Federated survival analysis with Cox regression

Statistical and machine learning models are extensively used in medical research. Sharing data among different centers and studies would help improve the accuracy and robustness of those models, but in the health sector this is often hindered due to ethical and privacy concerns associated with sensitivity of medical records. In ITEA project Secur-e-Health we focus on survival analysis and we propose an implementation of a Federated Proportional Hazard Cox model. In this way several institutions can collaborate to tune the model, without having to share data with other parties.

In the medical domain statistical models, and increasingly also machine learning models, are utilized for research, diagnosis and prognosis purposes. The development and enhancement of these models typically require access to a (relatively) large amount of data, which can pose a significant challenge for a single medical center.

Collaborating and sharing data among multiple institutions might make it feasible to create a comprehensive dataset; however, this is often difficult due to the highly confidential nature of medical records, containing personal information. Privacy enhancing technologies (in short PETs) can mitigate the corresponding risks for different parties to collaboratively use their data without exposing it and jeopardizing the privacy.

In this blog, we focus on a collaborative implementation of the Proportional Hazard Cox (PHC) model. The PHC model is used for survival analysis purposes, aiming to estimate the probability of a specific event occurring at a given time under certain conditions.

A common application is in clinical trials, where researchers want to determine whether an intervention statistically decreases the likelihood of an event (death or relapse, for example). To ensure the accuracy of the model, a PHC model can be jointly tuned by various medical centers, using data from multiple trials. This approach may even facilitate the incorporation of non-medical data (such as ethnicity, social economic status, medication adherence) from other organizations into the study.

The implementation we present here has been developed by TNO as part of the Secur-e-Health project, an international initiative that focuses on integrating state-of-the-art technologies, such as PETs, within the health domain. The overall goal is to facilitate collaboration and research while preserving the privacy and sensitivity of the data. The Dutch consortium includes, among others, also three medical centers (Amsterdam UMC, Erasmus MC, and UMC Utrecht) that contribute to shaping the use cases for this research.

Cox Model and Federated Learning: opportunities and challenges

The Cox Proportional Hazards (CPH) is a semi-parametric model returning the probability of experiencing an event (usually referred to failure) at any given point in time; this estimation is conditioned on a set of variables, or covariates, and on the absence of the event up to that point in time. The optimal parameters are usually determined using maximum likelihood estimation.

While a federated learning approach might seem tempting to jointly maximize the likelihood function using data distributed across various datasets, this approach is not as straightforward due to the form of the loss function of the PHC model, and specifically due to its non-separability (as explained in more detail below, or in [Andreux et al, 2020]). In the following paragraphs we offer a concise explanation of how federated learning is usually applied, and on the specificities of our case.

Federated learning provides a framework in which multiple parties can collaboratively train a model using their own data, without sharing the data itself. The rationale behind federated learning results particularly clear in the context of machine learning models obtained by optimizing the loss function applying stochastic gradient descent (SGD) methods.

SGD algorithms are approximations of the gradient descent algorithm: each optimization step is based on computing gradients of the loss function on a randomly selected subset of the dataset, rather than the entire dataset. In the Federated version of SDG, local minibatches of data, owned by a random subset of the parties, are selected at each step; the local gradients are calculated locally and then aggregated at central level, so to perform the next step of the optimization.

In case where the loss function is separable, it is possible to prove that the aggregated step corresponds to the step obtained if all the mini-batches were centralized. A loss function is considered separable when it can be expressed as a sum of terms that are independent of each other.

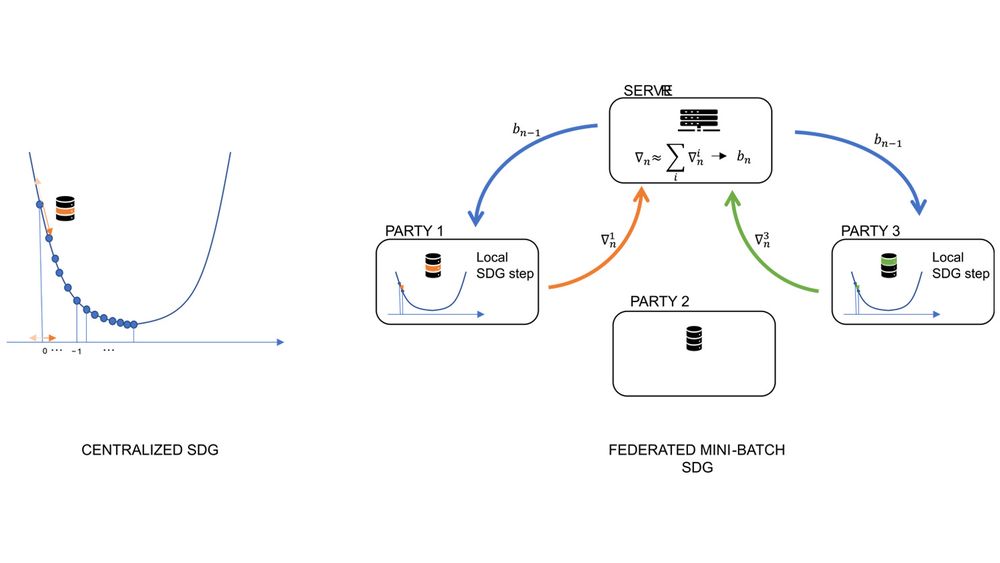
On the left a schema of the (stochastic) gradient descent method: the loss function is iteratively optimized by following the direction where the function decrease the most. In stochastic gradient descent (SDG) this optimal direction is calculated based on a subset of the data. On the right a schema of the federated mini-batch SDG: in each step of the optimization a subset of the parties locally calculate the optimal gradient; local gradients are then aggregated by the server to get the next iteration parameters.

Anyhow in the case of the CPH model the loss function takes the following form:

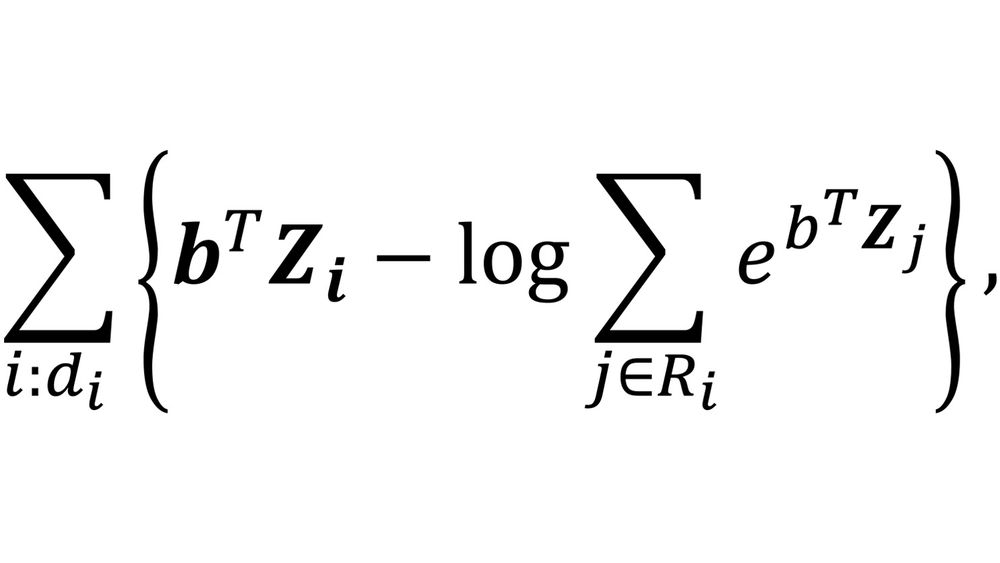
Where Z denotes the vector of covariates and b the coefficients to be optimized. The outer summation encompasses all entries of the datasets for which the event was observed (d=1), while the sum within the argument of the logarithm involves all the entries in the so-called risk set; the risk set comprises all individuals who have not yet experienced the failure event in the moment the i-th event occurs.

The crucial point to highlight here is that every term within the outer sum depends on all the other datapoints, via the risk set. This interdependence renders the loss functions non-separable, and this is poses a challenge to a straightforward application of federated learning.

Survival stacking approach

Fortunately, an alternative approach is available. In [Craig et al, 2021] it is proven that the task of computing the optimal CPH model parameters can be translated into a logistic regression problem.

The benefit of this transformation lies in the fact that the loss function of the logistic regression is separable, making it more suitable for a federated setting.

A typical dataset for a survival analysis problem consists of logs in the form {(ti, di, Zi )}: t indicates the time; d is a binary variable, with value 1 if a failure happened, and value 0 in case of censoring (if for example the patient left the study); Z is the set of corresponding covariates.

For each failure event, we define the risk set Ri as the set of individuals still in the study at time ti, who have not yet experienced the failure. We build the so-called stacking dataset by adding a data block for each risk set. Each entry of this new dataset contains covariates, binary variables indicating the corresponding risk set, and a binary column for failure. The picture shows a visual representation of the process, that is also nicely explained in this online available video.

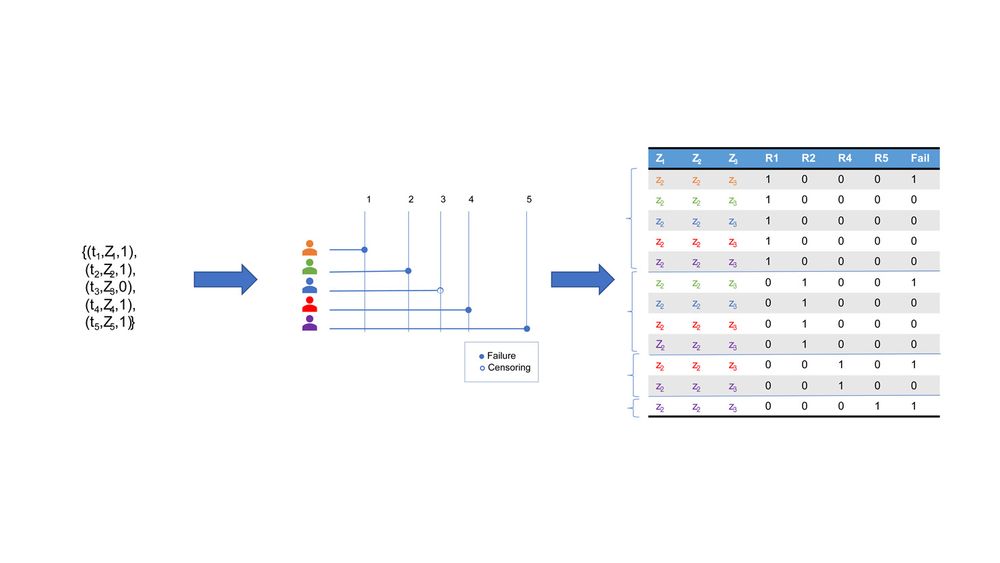
A visual representation of how to build the stacking dataset from a survival analysis dataset. In the example we have 4 failure events, and one censoring. For each failure, a risk set is identified, and a block of the new stacking dataset is built, including the covariates of the people in the risk set, the indication of which risk set the rows refer to, and the failure variable.

With the data in this format, a classification problem can be formulated using the original covariates and the risk sets variables as independent variables, and the failure column as target. In essence, we are training a classifier to predict failure occurrence with given covariates and in a specific time window.

Empirical results show that the optimal parameters for the covariates variables of a logistic regressor classifier trained on the stacking datasets closely resemble the optimal parameters for the CPH loss function. This connection between the classification problem and the CPH problem has also theoretical foundation in previous literature, where discrete Cox models converge to the logistic regression model. For more details we refer to in [Craig et al, 2021], [Andreux et al, 2020]

These results offers several opportunities:

• First, a logistic regression model can be optimized within a federated learning setting. After each party generates its stacking data, federated learning can be applied straightforwardly. While some communication about the time steps used to identify risk sets is necessary for coherent datasets, this doesn't compromise personal information.
• Furthermore, logistic regression has already been studied in vertically partitioned settings, for example in [Zhao et al, 2023], where parties own different data about the same individuals; combining these results with the stacking approach would lead to an implementation of a vertically distributed Cox model. This would cover cases where some non-medical variables, owned by external organizations, are used as covariates. We plan to explore this in the next phase of the project.
• Finally, this method naturally adapts to extensions of the CPH model where the covariates are functions of time. These models are sometime referred to as time dependent Cox models, and capture the situation where multiple entries for the same patient are recorded, possibly with varying values of the covariates. In the stacking approach, a single patient’s clinical history corresponds to multiple lines, one for each time window in which the patient remains in the study. Changes in the value of the covariates would be therefore naturally represented.

Our implementations and experiments

During the project we have implemented two standalone functionalities, that have been published under open source license here: the Federated Logistic Regression model (for horizontally distributed data), and the Federated Cox model, which is based on the stacking approach described earlier.

The Federated Cox Model includes a method to generate the stacking dataset in the distributed setting, followed by the application of the Federated Logistic Regression. The Federated Logistic Regression offers the option to use either a regular stochastic gradient descent solver or second-order solvers, see for example [Safaryan et al, 2022]; second-order solvers, while more communication-intensive, have proven to yield better results in the application to the Cox model.

We have tested our approach using two open source datasets, the Rotterdam Tumor Bank and the Colon datasets, and randomly split the data between 2 parties.

To validate the results we have compared the parameters obtained with the Federated Cox Model with the parameters that we would get in a central setting. In a central setting two options are available: either optimizing the Cox Model loss function directly (we have used the python LifeLines implementation), or applying the stacking approach.

We also have evaluated the Cox models corresponding to the different sets of parameters using the concordance index (or in brief C-index), a widely used metric for survival models checking whether the model reflects the relative time order of the failure events.

Those first results are promising: both the optimal parameters and the C-index obtained with the federated stacking approach reasonably approximate the results in the central setting.

Conclusions and next steps

This project contributes to create tools that foster secure collaboration among various medical centers, thereby enhancing the potential of their research and data. In the next phase, we will expand the implementation to a vertically distributed setting and conduct additional testing with diverse datasets. One of our partners in the consortium, Linksight, is also actively working to bring the software developed in the project to a market-ready level.